I've poked fun at AI a couple of times in these articles mostly because I think it's funny that tech people treat generative models as the magic fix-all tool for literally everything. But what these vibe coders and B2B SaaS enjoyers might not realize that we've had our own version of "AI"if you think about it, AI is a nonlinear model being propagated forwards, which is also what control theory is! for nearly 200 years called control theory.
Unlike modern AI which shines when rules aren’t known ahead of time (recognizing objects, understanding languages, or counting the number of r’s in the word strawberries), control theory is designed for the physical world where the rules are well-defined. Motors, temperatures, and mechanical systems are part of well-defined, physics-driven problems where the inputs, outputs, and desired behaviors are already known. And for real-world problems, you do want fast, predictable, repeatable math as opposed to querying something to a data center in Alaska and praying that it doesn’t hallucinate.

Even if we manufactured robots on a well-oiled assembly line, no two would come out exactly the same. Tiny differences in friction, weight, or alignment mean they’ll all behave a little differently, and in some environments, even the slightest error can have serious consequences. Just like tuning a guitar before you play, we need to “tune” each robot before it moves if we want it to hit the right notes. One of the most common tools for that job is something called a PID controller.
A PID controller is a feedback system that helps a robot stay on track when it's trying to move in any form - like rotating a joint, holding an arm steady, or following a line on the floor. PID stands for Proportional-Integral-Derivative, and if that phrase triggers traumatic memories from calculus, don't worry! In practice, it's a lot simpler than it sounds! Essentially, anytime you try to move to a certain position, a PID controller is constantly using the following 3 'metrics' to get there in a more efficient way:
P
how wrong you are right now
I
how long you've been wrong
D
if you're about to be more wrong
Let's Chill Out
It's a lot easier to visualize control systems with an everyday item, and we don't even need to use an example with a robot or one that involves motion. Take a crappy A/C unit you snatched off Facebook Marketplace for $40. It does its best to blast cold air into your room until the room hits the temperature you set, but it's not great. So let's design a PID controller to keep your room cool without the $6,000 electric bill.

From that simple example, we can already define some terms if this was a real control system. The plant (what we're controlling) is your room. The setpoint is the temperature you want (say, 70°F). The process variable is the actual room temperature right now (around 74°F). The control output is what the A/C can do: blow cold air to bring the temperature down.
- Your setpoint, r(t) = desired room temperature (70°F)
- Process variable, y(t) = actual room temperature (74°F)
- Error, e(t) = y(t) − r(t) = how far off you are. So at time = 0, it wouid be 74 - 70 = 4°F
- Control output, u(t) = A/C effort. This will usually be a decimal between 0 - 1, as a ‘duty cycle’ or % power
- Plant, G(s) = room thermal response (air + walls)
- Disturbance, d(t) = heat from sun, people, appliances, open door, etc. Disturbance is really just any other variables we don’t technically account for, but plan for.
- Kp = proportional gainKp also stands for proportional coefficient. Mathematicians famously can't spell and thought that the word 'coefficients' starts with a 'K'. This determines how strongly the controller reacts to the current error. Think of Kp as the "muscle" of your controller.
- Ki = integral gain. Determines how strongly the controller reacts to the accumulated (past) error. Think of Ki as the "memory" of your controller.
- Kd = derivative gain. Determines how strongly the controller reacts to the predicted future error (based on rate of change). Think of Kd as the "brakes" of your controller.
Note: You'll notice that everything has an (t) attached to it - this just means that all of our variables are a function of time. Time also happens to be a great metric for how well our controller is working!
Now, everything comes together in a neat equation like so:
… but the important thing is really this picture below:
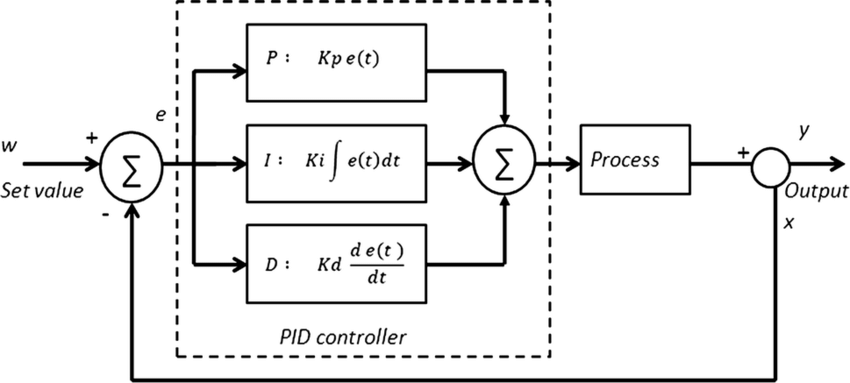
This is a block diagram, and aside from being a diagram containing blocks is also a schematic that represents a control system in a more digestible form. We start on the left with our setpoint, or input (70°F) entering the diagram on the left. That passes through the controller, which uses our variables to determine what small change our A/C should make. At the end on the right, if our setpoint hasn’t been met yet, the loop restarts and passes through the controller again, making tiny adjustments until the room has cooled down to the desired temperature. The key takeaway here is that the controller doesn’t get it ‘right’ on the first attempt. A PID controller iterates constantly by correcting and adjusting itself until our process is finished.
A/C PID Simulator
Before hopping straight into this incredible simulator, I did simplify the model a bit so that you can see the direct effects of each gain on the system. Under the hood I switched to a slightly richer A/C room with walls (two thermal masses = gentle second-order plant), so the system is a bit more realistic. Try messing around with each of the three gains to see how they affect the system in real time!
Control Parameters
System Response
Air Temperature vs Time
Control Effort (0–100%)
Performance Metrics (hover over these to see what they mean!)
Tuning Gone Wrong
Usually, tuning a PID controller isn't as easy as I made it out to be. If the A/C's "PID brain" isn't tuned correctly, things could get messy:
Too Much Gain
Too Little Gain
Once you've got the gains in the ballpark, you'll notice the overall shape of how the room approaches the target can look very different:
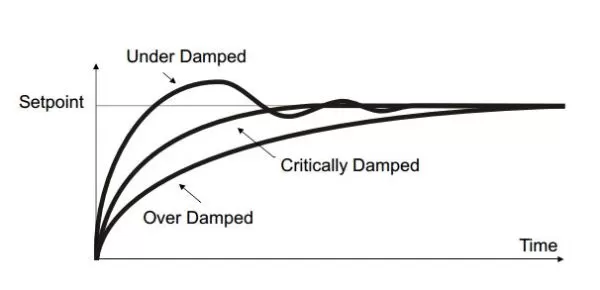
Underdamped
The A/C is too aggressive. The room temp overshoots below 70°F, then bounces above, then below again. It's unstable, like a shower that keeps swinging between freezing and boiling.
Overdamped
The A/C is too cautious. The room crawls toward 70°F so slowly that it feels like it never gets there. Stable, but painfully sluggish.
Critically Damped
The Goldilocks zone. The room cools down quickly without overshooting and settles smoothly right on 70°F.
Cool math, but what is the point of all this?
Embarrassingly, this is one of my favorite subjects in robotics, but I still went through two semesters of control theory in college without really understanding one simple question - what is a controller? In my head (and likely yours right now), it was just a bunch of math, graphs, and variables that magically got plugged into a circuit board.
It wasn't until I had an internship designing PID controllers in Python for a robot when everything clicked -
it's pretty much a while() loop. If you're not a software person, that means it's just a loop
that runs thousands of times with incremental changes until what you want to happen, well, happens. And tuning
is just the process of making that process more efficient. Yes, there's a lot of math that goes into this, but
at its core PID control means using live feedback to do something better.
Even if you're not a software person, take a gander at this code block. It's a bare-bones version of a PID loop used to command a motor to a certain rpm (revolutions per minute, a common way to describe motor speed). It's pretty similar to what you might see in a real robot control script!
# initializing the value of each gain
Kp = 0.4
Ki = 0.1
Kd = 0.05
target = 1000.0 # desired RPM (setpoint, or your target speed)
integral = 0.0
prev_error = 0.0
while True:
# 1. Measure process variable, or current speed
current = read_rpm()
# 2. Calculate error
error = target - current
# 3. ID terms
integral += error
derivative = error - prev_error
# 4. Calculate control effort
output = Kp*error + Ki*integral + Kd*derivative
# 5. Apply to motor
set_motor(output)
# 6. Save state for next loop
prev_error = errorPID is pretty great, but real systems are never perfect. Disturbances sneak in, like sunlight heating your room, a door opening, or a gust of wind hitting a drone. A PID controller can correct for these, but only after they’ve already happened. It reacts, it doesn’t anticipate.
The future of control theory might blend feedback loops with self-learning systems to fill in some of the gaps, but at the end of the day PID is an integral part of robotics and physical systems that won’t be going anywhere. In future lessons, we’ll learn about more complex types of controllers that try to predict the future of our system in interesting ways.